The Power of Product Notation: A Comprehensive Exploration of the Big Product in LaTeX
Related Articles: The Power of Product Notation: A Comprehensive Exploration of the Big Product in LaTeX
Introduction
In this auspicious occasion, we are delighted to delve into the intriguing topic related to The Power of Product Notation: A Comprehensive Exploration of the Big Product in LaTeX. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
The Power of Product Notation: A Comprehensive Exploration of the Big Product in LaTeX

The realm of mathematics is replete with elegant notations that enable concise expression of complex ideas. Among these, the "big product" notation, often denoted by a capital pi (Π), stands as a powerful tool for representing the product of a sequence of numbers. This notation, seamlessly integrated into the LaTeX typesetting system, allows mathematicians and researchers to express intricate mathematical expressions with clarity and efficiency.
Understanding the Essence of the Big Product
The big product, like its counterpart, the big sum (Σ), operates on a sequence of terms. It essentially captures the result of multiplying all the terms in the sequence, adhering to a specified range. This range, typically defined by a lower and upper limit, dictates the extent of the multiplication.
For instance, consider the expression:
Πi=1n ai
This notation signifies the product of all terms ai, where i ranges from 1 to n. In simpler terms, it represents the multiplication:
a1 a2 a3 … an
Benefits of Using the Big Product Notation
The big product notation offers numerous advantages, making it an indispensable tool in various mathematical contexts:
- Conciseness and Clarity: It provides a compact and unambiguous way to represent complex multiplications, significantly enhancing the readability of mathematical expressions.
- Generalization and Flexibility: The notation readily accommodates any sequence of terms, allowing for the representation of products involving variables, functions, or even other mathematical expressions.
- Simplification of Calculations: The notation facilitates the manipulation and simplification of expressions involving multiple products, often leading to more streamlined solutions.
- Mathematical Rigor: The big product notation fosters mathematical precision and consistency, ensuring accurate representation of products within a defined range.
Applications of the Big Product Notation
The big product notation finds extensive applications across diverse mathematical fields, including:
- Calculus: It plays a crucial role in defining and evaluating definite integrals, where the product of infinitesimal elements is essential.
- Combinatorics: The notation is instrumental in representing and calculating combinations and permutations, often involving products of factorials.
- Number Theory: The big product is used to express properties of integers, such as the prime factorization of a number.
- Linear Algebra: It finds applications in representing determinants of matrices and other matrix operations.
- Probability and Statistics: The notation is employed in calculating probabilities and expected values involving multiple events.
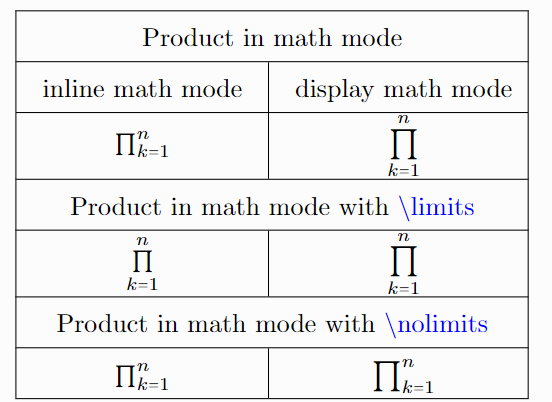
Implementing the Big Product in LaTeX
LaTeX, the powerful typesetting system widely used in academia and scientific publishing, provides a straightforward way to incorporate the big product notation:
-
Command: The command
prodis used to generate the capital pi symbol (Π). -
Limits: The lower and upper limits are specified using the
_...^...notation, placed after the command. - Terms: The terms to be multiplied are placed within the limits.
Example:
To typeset the expression Πi=1n ai in LaTeX, the following code is used:
prod_i=1^n a_iThis code will render the expression with the correct notation and formatting.
FAQs About the Big Product in LaTeX
Q: What is the difference between the big product and the big sum?
A: While both notations represent operations over sequences, the big product involves multiplication of terms, whereas the big sum involves their addition. The big product is denoted by Π, while the big sum is denoted by Σ.
Q: Can the limits of the big product be variables?
A: Yes, the limits can be variables, allowing for flexibility in defining the range of multiplication.
Q: How do I typeset the big product with a different symbol instead of Π?
A: LaTeX provides alternative symbols for the big product, such as coprod and bigodot. You can replace prod with these commands to achieve the desired symbol.
Q: Can I use the big product to represent products over infinite sequences?
A: While the big product notation is typically used for finite sequences, it can be extended to infinite sequences using the concept of limits.
Tips for Using the Big Product in LaTeX
- Consistency: Maintain consistency in the format and placement of the limits and terms for improved readability.
- Spacing: Ensure proper spacing between the symbols, limits, and terms to avoid crowding.
- Clarity: Use clear and concise notation to enhance the understanding of the mathematical expressions.
- Preview: Preview the LaTeX code before finalizing the document to ensure accurate rendering of the big product notation.
Conclusion
The big product notation, seamlessly integrated into the LaTeX typesetting system, provides a powerful and efficient way to represent products of sequences. Its conciseness, flexibility, and ability to simplify calculations make it an indispensable tool in various mathematical domains. By understanding and effectively utilizing the big product notation, mathematicians and researchers can express complex mathematical ideas with clarity, precision, and elegance.
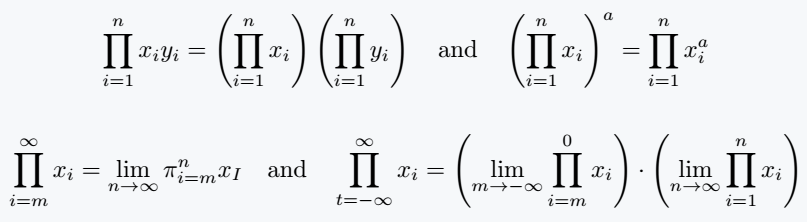
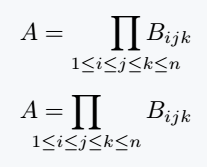
![[SOLVED] Help using cumulative kronecker product notation in LaTeX? ~ TeX - LaTeX ~ AnswerBun.com](https://i.stack.imgur.com/VROIz.png)


Closure
Thus, we hope this article has provided valuable insights into The Power of Product Notation: A Comprehensive Exploration of the Big Product in LaTeX. We appreciate your attention to our article. See you in our next article!
